Multimodal Distribution in Image or Text domain
Q: What does "multimodal distribution" mean in computer vision literature (eg. image-to-image translation)?
While reading papers on conditional image generation using generative modeling (eg. "Toward Multimodal Image-to-Image Translation" by Zhu et al (NIPS 2017)), I wasn't clear what was meant by "one-to-many mapping" between input image domain and output image domain, "multimodal distribution" in the output image domain, or "multi-modal outputs" (eg. Quora).
Definition
In statistics, a
multimodal distributionis a continuous probability distribution with two or more modes (distinct peaks; local maxima) - wikipedia
| (single-variable) bimodal distribution | bivariate multimodal distribution |
|---|---|
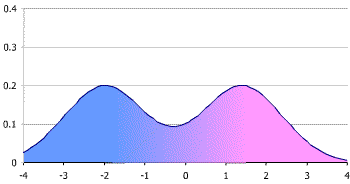 |
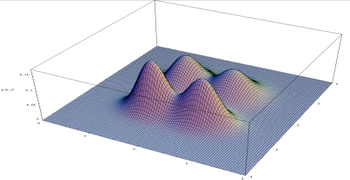 |
In high-dimensional space (such as an Image domain: \(P(X)\) where X lives in \(d\)-dim space where \(d\) is the number of pixels, eg. \(32x32=1024\). If each pixel \(X_i\) takes a binary value (0 or 1), the size of this image domain is \(2^{1024}\). If each pixel takes an integer value \(\in [0,255]\), then the size of this image domain is \(256^{1024}\). This, by the way, is too big to compute for Mac's spotlight:

What it means by saying "the distribution of (output) image is multimodal" is to say, there are multiple images (ie. realization of the random variable (vector) X) with the (local) maxima value of the probability. In Figure below, the green dots represent the local maxima, ie. modes of the distribution. The configurations (ie. specific values/realizations) that achieves the (local) maximum probability density are the "probable/likely" images.


So, given one input image, if the distribution of the output image random variable is multi-modal, the standard problem of
Find \(x\) s.t. \(\underset{x \in \mathcal{X}}{\arg\max} P(X)\) (\(\mathcal{X}\) is the image space)has multiple solutions. According to the paper (Toward Multimodal Image-to-Image Translation), many previous works have produced a "single" output image as "the" argmax of the output image distribution. But this is not accurate if the output image distribution is multi-modal. We would like to see/generate as many of those argmax configurations/output images. One way to do so, is by sampling from the output image distribution. This is the paper's approach.
Multimodal distribution as the distribution over the space of target domains [Domain adaption/transfer leraning]
So far, I viewed the multimodal distribution as a distribution over a specific domain (eg. Image domain), and the random variable corresponded to a realization, eg. an observed/sampled/output image instance. However,